
 反差 母狗
反差 母狗
看雪CTF快讯:
第八题无东谈主破解生效
导语欺压第八题今天中午罢手,无东谈主攻破。第八题的作家ccfer以0东谈主攻破的收货生效登上第一位。

挫折方名次保捏不变
当今仅剩只剩下终末一题——九层妖塔,这亦然变嫌名次的终末一次契机!
能否有东谈主绝地反击?获得终末的三个限额?
本届比赛又是否会出现两个详实方冠军?让咱们静瞻念其变!
接下来让咱们通盘来望望第八题的联想念念路。
看雪评委netwind点评该题西颦东效,是左证冲突傅立叶变换及逆变换在时域和频域的关系和性质构造的一个破解题目。题目中内置了一组频谱Xk和一组冲突采样值xn。用注册码背面一部分(C部分)当作频域梳妆滤波器,从频率Xk中过滤掉噪声重量后再作念快速傅立叶逆变换(IFFT)得到的时域信号,与xn去除周期方波纷扰(由注册码前边一部分A和中间部分B生成)的时域信号进行匹配,来考据注册码是否有用!
第八题作家简介ccfer,从看雪001论坛开赴点学习脱壳逆向,产生酷好后毁灭从事多年的电力系统继电保护行业,转行到软件安全,感谢论坛多年来提供的学习环境,祝看雪论坛越办越好。
第八题联想念念路系统需求:WIN64
注册生效教唆:Good job!
正确注册码:
E36F74E4D69ABAF222B0F684416F121FD5AFC1BE97B0FFE28118AA1C2D2C00DEF63729C8
注册码步骤:
AAAAAAAAAAAAAAAAAAAAAAAABBBBBBBBBBBBBBBBBBBBBBBBCCCCCCCCCCCCCCCCCCCCCCCC,可分为A,B,C三个部分,调遣成16进制后,每部分对应12个字节。
题目摘记期骗冲突傅立叶变换及逆变换在时域和频域的关系和性质构造的一个crackme;
维基百科里解释:
冲突傅里叶变换(Discrete Fourier Transform,缩写为DFT),是傅里叶变换在时域和频域上齐呈冲突的神色,将信号的时域采样变换为其DTFT的频域采样。在神色上,变换两头(时域和频域上)的序列是有限长的,而试验上这两组序列齐应当被合计是冲突周期信号的主值序列。即使对有限长的冲突信号作DFT,也应当将其看作其周期延拓的变换。在试验应用中常常弃取快速傅里叶变换缱绻DFT。
题目中内置了一组频谱Xk和一组冲突采样值xn,频谱涵盖1到96次谐波,采样点数是256点;
Xk中谐波重量分两组,一组是信号量,一组是噪声量;xn则重迭了周期方波纷扰;
用注册码C部分当作频域梳妆滤波器,从频率Xk中过滤掉噪声重量后再作念快速傅立叶逆变换(IFFT)得到的时域信号,与xn去除周期方波纷扰(由注册码A和B部分生成)的时域信号匹配,那么注册码即是有用的;
考据关系不错这么神色:FrequencyDomainFilter(IFFT(Xk), C) = TimeDomainFilter(xn, A, B);
试验题目中A部分有2个解,B部分有17个解,A和B组合起来共有34组周期方波波形,其中唯有一种是好像匹配生效的,手工穷举即可完成。
另外为了增多分析难度,题目中的数值存储齐作念了简便的移位交换加密,运算前读取内存中的变量解密,运算后再加密保存到内存变量中。
相关IFFT的运算莫得用系统的浮点数,用的是定点数,把int64主张成高32位的整数部分和低32位的极少部分,本体即是数值的缩放,极少点看不看得见并不伏击。
所用的正弦余弦函数齐是预先缱绻好的,用的技巧径直查表了。
算法神色底下内容中不加0x前缀的均默示10进制数
1. 第一部分A的算法是二次剩余问题,用于纷扰时域采样值的偶数项。
这部分比拟简便,极度的场地在于平淡模的结束莫得用到乘法,旨趣如下:
轻易考取一个远浩大于p的常数F,常数G=F*F*F*F-F+1, 常数H=F*F*F*F+F*F-F+1
g = G % ((A % p) + F) % p
h = H % ((A % p) + F) % p
不错讲授出:
g = (A*A*A*A + A + 1) % p
h = (A*A*A*A + A*A + A + 1) % p
于是:
(h – g) % p = A * A % p
无须乘法就求出了A的平淡模(想了解这个念念路的降服,可自行前去阅读h**p://www.matrix67.com/blog/archives/5362)
回到刻下题目里,具体问题是求解底下一个二次剩余问题:
p = 44876614366229365187800397851
r = 14995684705179149819785261106
A * A % p = r
A用NTL大数库现成的函数A = SqrRootMod(r, p)可径直求解,或者用RDLP缱绻器径直算
A = 41150248829223493762924441571,同期(p – A)亦然方程的解
因此A部分有2个解:
0x84F6B022F2BA9AD6E4746FE3
0x0C0A609888EB889D7AF28838
2. 第二部分B的算法是个实施型的pell方程,用于纷扰时域采样值的奇数项
把B隔断两半各6字节长度的x和y。
具体问题是求底下方程的整数解:
5*x*x - 3*y*y = 2
方程解法可用Largrange连分式法或矩阵法,矩阵法的话不错参考下图中的定理:
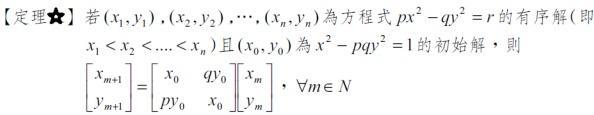
也即是先求出x*x - 3*5*y*y = 1的一个启动解,径直不雅察或小鸿沟穷举可得启动解:(4,1)
相通5*x*x - 3*y*y = 2的启动解也很容易得到:(1,1)
再求出变换矩阵:
4 3
5 4
然后方程的总共解齐不错顺次缱绻得到了:
//示例算法,要更多的解__int64会溢出,应该用大数结束,不外就此题而言用__int64也实足了
int i;
__int64 t;
__int64 x = 1;
__int64 y = 1;
for (i=0;i<20;i++)
{
t = x * 4 + y * 3;
y = x * 5 + y * 4;
x = t;
cout << "x=" << x << endl;
cout << "y=" << y << endl;
}
方程在6字节的规则的长度鸿沟内有17组解:
{0x000000000001,0x000000000001}
{0x000000000007,0x000000000009}
{0x000000000037,0x000000000047}
{0x0000000001B1,0x00000000022F}
{0x000000000D51,0x000000001131}
{0x0000000068D7,0x000000008759}
{0x000000033967,0x000000042997}
{0x000000196261,0x00000020C55F}
{0x000000C7D9A1,0x000001020161}
{0x000006256AA7,0x000007EF45A9}
{0x000030637B97,0x00003E782BE7}
{0x00017CF67211,0x0001EBD2198F}
纪湘视频在线观看{0x000BB75014F1,0x000F2018A091}
{0x005C3D8A3577,0x007714F2EAF9}
{0x02D6350196C7,0x03A9877EB737}
{0x16556A8280C1,0x1CD52702CEBF}
{0xAFD51F126F41,0xE2FFB097BEC1}
3. 第三部分C的算法是IFFT,亦然本题的中枢考据
内置频谱Xk经过C值二进制位屏蔽掉噪声频率重量,作念IFFT还原到时域冲突信号,再重迭A和B生成的方波,与内置xn的方差值要是小于一定鸿沟,则匹配生效。
刻下的采样频率关于此纷扰周期方波来说不成欢畅期奈奎斯特采样的定理的条款(采样频率fs.max大于信号中最高频率fmax的2倍),是以不必滤除纷扰方波径直对xn作念FFT得到的成果不会对频谱重量产生本体变化(虽然一定要穷举A和B组合的34组方波滤除纷扰也不错,仅仅冠上加冠,成果一样),
这么得到的频谱和内置的Xk对比,看Xk中短缺了哪些频率重量,从而确定C中为1的位。
这部理解法代码参考单独附件文献solvefft.cpp
为了更形象直不雅,这部分也不错用matlab来解,示例(输入的数值齐放大了10000倍,便捷不雅察也省去了极少点,虽然这些数值需要有个移位解密历程才调得到):
N=256;
n=0:N-1;
xn=[513227,352677,120365,184774,16616,165078,350263,17761,-4424,178812,53257,84570,115610,-21613,64830,133790,42358,21409,40276,113004,128339,9542,13155,65564,17442,15923,34815,42483,68112,-24713,-132308,-30929, ...
110352,105703,88405,84805,43179,83137,101041,-22196,-15975,93945,59842,1587,-26834,-37987,4106,-56684,-102642,5277,63189,116651,134388,5713,50300,143057,7244,-3068,68244,-3911,48427,106580,-10550,-23592, ...
41109,-16189,-82771,-43512,12923,-12783,-10204,20307,-58625,-48523,83577,37311,-39703,22208,22715,-1343,26426,-6892,-7910,80561,86954,31208,74282,97360,-17630,-46986,66679,98463,74427,64015,2996,-24930, ...
3154,32702,114887,126063,-18483,-81642,4830,48422,38061,39947,-9388,-62939,-11777,29075,24050,75408,80716,57844,125591,93868,-11953,3692,-8309,-19813,78883,68528,2542,34029,51422,102745,136347,1472,-67837, ...
-14248,-20978,17723,63960,-27387,-39928,65692,75404,52242,63656,24449,-3569,-7254,-61102,-75174,-9543,38489,79760,123357,105866,49227,8961,6916,64732,113072,44956,-55689,-36193,31419,66498,92245,24032, ...
-60894,-8238,-18740,-56942,104151,145732,-21749,-30317,14427,-21412,18577,57060,30899,16957,26605,46860,29167,39755,59726,-3362,66867,157937,25240,54883,156699,-7576,9213,176611,115856,81562,47209,-42200, ...
42500,65973,-7166,30905,30519,37321,54072,-28335,-24790,-26860,-85316,2737,29266,23895,162546,138940,52855,106579,31831,-41245,22391,12292,33032,71533,-17532,-21898,36364,-20140,-58593,-36459,21681,134673, ...
124499,19952,27629,21199,-5272,80325,37049,-56557,64342,42711,-105213,4749,40448,-56697,24845,22456,-50996,29341,29191,-48154,-70042,-38159,6590,-123000,-165431,6374,-56271,-127370,-179473,-467218,-145137];
Xk=[0+0i,0-20000i,122-9999i,981-19975i,368-9993i,490-9987i,1226-19962i,2934-19783i,1715-19926i,3901-19615i,2204-19878i,1224-9924i,5334-19275i,2902-9569i,6273-18990i,6737-18830i, ...
3660-19662i,3826-9238i,2071-9783i,2191-9757i,8992-17864i,9427-17638i,4928-8700i,2667-9637i,10699-16897i,5805-19138i,5758-8175i,11913-16064i,6506-18912i,6737-18830i,6968-18746i,13431-14819i, ...
3713-9285i,14142-14142i,7242-6895i,4052-9142i,15144-13063i,15460-12687i,4386-8986i,16064-11913i,8175-5758i,4713-8819i,16897-10699i,4928-8700i,8700-4928i,17638-9427i,8932-4496i,18079-8551i, ...
5453-8382i,18477-7653i,9329-3598i,9415-3368i,5857-8104i,5956-8032i,9637-2667i,19400-4859i,12497-15614i,12687-15460i,6438-7651i,9891-1467i,6624-7491i,13431-14819i,9972-735i,19975-981i, ...
6983-7157i,9999+0i,9996+245i,9987+490i,7326-6806i,7409-6715i,9924+1224i,15144-13063i,19705+3419i,9807+1950i,7807-6248i,19400+4859i,7958-6055i,8032-5956i,16209-11715i,18830+6737i, ...
18659+7197i,18477+7653i,9142+4052i,18079+8551i,17864+8992i,8819+4713i,17401+9857i,8577+5141i,8760-4821i,17638-9427i,17752-9210i,8032+5956i,8986-4386i,9039-4275i,9091-4164i,14819+13431i, ...
14484+13790i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i, ...
0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i, ...
0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i, ...
0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i,0+0i, ...
14484-13790i,14819-13431i,9091+4164i,9039+4275i,8986+4386i,8032-5956i,17752+9210i,17638+9427i,8760+4821i,8577-5141i,17401-9857i,8819-4713i,17864-8992i,18079-8551i,9142-4052i,18477-7653i, ...
18659-7197i,18830-6737i,16209+11715i,8032+5956i,7958+6055i,19400-4859i,7807+6248i,9807-1950i,19705-3419i,15144+13063i,9924-1224i,7409+6715i,7326+6806i,9987-490i,9996-245i,10000+0i, ...
6983+7157i,19975+981i,9972+735i,13431+14819i,6624+7491i,9891+1467i,6438+7651i,12687+15460i,12497+15614i,19400+4859i,9637+2667i,5956+8032i,5857+8104i,9415+3368i,9329+3598i,18477+7653i, ...
5453+8382i,18079+8551i,8932+4496i,17638+9427i,8700+4928i,4928+8700i,16897+10699i,4713+8819i,8175+5758i,16064+11913i,4386+8986i,15460+12687i,15144+13063i,4052+9142i,7242+6895i,14142+14142i, ...
3713+9285i,13431+14819i,6968+18746i,6737+18830i,6506+18912i,11913+16064i,5758+8175i,5805+19138i,10699+16897i,2667+9637i,4928+8700i,9427+17638i,8992+17864i,2191+9757i,2071+9783i,3826+9238i, ...
3660+19662i,6737+18830i,6273+18990i,2902+9569i,5334+19275i,1224+9924i,2204+19878i,3901+19615i,1715+19926i,2934+19783i,1226+19962i,490+9987i,368+9993i,981+19975i,122+9999i,0+20000i];
plot(n(1:255),xn(1:255)/10000);
先望望xn的时域波形,没啥用,即是想望望它长啥样:
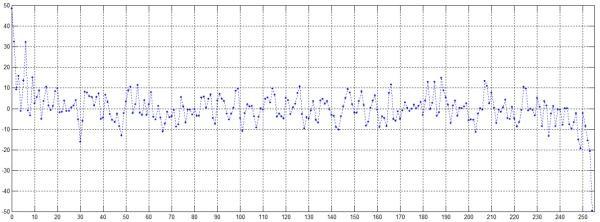
Xk1=fft(xn)/N*2;
plot(n(1:96),abs(Xk1(1:96)/10000),n(1:96),abs(Xk(1:96))/10000);
然后画出对比频谱图(径直画出的是带线条的,咱们只护理冲突的点,是以修改一下贱露竖立:两条线的LineStyle选none,Marker一条选绿色o,另一条选红色x):
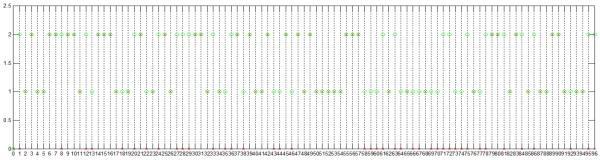
图中绿o内置的频谱重量幅值,红x是径直对内置xn经FFT后得到的频谱重量幅值,不错看出绿o涵盖了1到96次谐波总共的频率重量,而红x是有一部分频率重量的幅值是0的,默示不含有此频率谐波。
左证落在横坐标轴上(甩掉0是直流重量)从96到1的红x由高位到低位组成的大数就能得到注册码的C部分0xC82937F6DE002C2D1CAA1881
考据成果:把ABC各式组合拼起来(提防所用的大数小端在前,字节序列要翻转)就得到了34个的待定的注册码:
E36F74E4D69ABAF222B0F6840100000000000100000000008118AA1C2D2C00DEF63729C8
E36F74E4D69ABAF222B0F6840700000000000900000000008118AA1C2D2C00DEF63729C8
E36F74E4D69ABAF222B0F6843700000000004700000000008118AA1C2D2C00DEF63729C8
E36F74E4D69ABAF222B0F684B101000000002F02000000008118AA1C2D2C00DEF63729C8
E36F74E4D69ABAF222B0F684510D000000003111000000008118AA1C2D2C00DEF63729C8
E36F74E4D69ABAF222B0F684D768000000005987000000008118AA1C2D2C00DEF63729C8
E36F74E4D69ABAF222B0F6846739030000009729040000008118AA1C2D2C00DEF63729C8
E36F74E4D69ABAF222B0F6846162190000005FC5200000008118AA1C2D2C00DEF63729C8
E36F74E4D69ABAF222B0F684A1D9C70000006101020100008118AA1C2D2C00DEF63729C8
E36F74E4D69ABAF222B0F684A76A25060000A945EF0700008118AA1C2D2C00DEF63729C8
E36F74E4D69ABAF222B0F684977B63300000E72B783E00008118AA1C2D2C00DEF63729C8
E36F74E4D69ABAF222B0F6841172F67C01008F19D2EB01008118AA1C2D2C00DEF63729C8
E36F74E4D69ABAF222B0F684F11450B70B0091A018200F008118AA1C2D2C00DEF63729C8
E36F74E4D69ABAF222B0F68477358A3D5C00F9EAF21477008118AA1C2D2C00DEF63729C8
E36F74E4D69ABAF222B0F684C7960135D60237B77E87A9038118AA1C2D2C00DEF63729C8
E36F74E4D69ABAF222B0F684C180826A5516BFCE0227D51C8118AA1C2D2C00DEF63729C8
E36F74E4D69ABAF222B0F684416F121FD5AFC1BE97B0FFE28118AA1C2D2C00DEF63729C8
3888F27A9D88EB8898600A0C0100000000000100000000008118AA1C2D2C00DEF63729C8
3888F27A9D88EB8898600A0C0700000000000900000000008118AA1C2D2C00DEF63729C8
3888F27A9D88EB8898600A0C3700000000004700000000008118AA1C2D2C00DEF63729C8
3888F27A9D88EB8898600A0CB101000000002F02000000008118AA1C2D2C00DEF63729C8
3888F27A9D88EB8898600A0C510D000000003111000000008118AA1C2D2C00DEF63729C8
3888F27A9D88EB8898600A0CD768000000005987000000008118AA1C2D2C00DEF63729C8
3888F27A9D88EB8898600A0C6739030000009729040000008118AA1C2D2C00DEF63729C8
3888F27A9D88EB8898600A0C6162190000005FC5200000008118AA1C2D2C00DEF63729C8
3888F27A9D88EB8898600A0CA1D9C70000006101020100008118AA1C2D2C00DEF63729C8
3888F27A9D88EB8898600A0CA76A25060000A945EF0700008118AA1C2D2C00DEF63729C8
3888F27A9D88EB8898600A0C977B63300000E72B783E00008118AA1C2D2C00DEF63729C8
3888F27A9D88EB8898600A0C1172F67C01008F19D2EB01008118AA1C2D2C00DEF63729C8
3888F27A9D88EB8898600A0CF11450B70B0091A018200F008118AA1C2D2C00DEF63729C8
3888F27A9D88EB8898600A0C77358A3D5C00F9EAF21477008118AA1C2D2C00DEF63729C8
3888F27A9D88EB8898600A0CC7960135D60237B77E87A9038118AA1C2D2C00DEF63729C8
3888F27A9D88EB8898600A0CC180826A5516BFCE0227D51C8118AA1C2D2C00DEF63729C8
3888F27A9D88EB8898600A0C416F121FD5AFC1BE97B0FFE28118AA1C2D2C00DEF63729C8
终末能熟谙通过的是中间阿谁绿色的。

温馨教唆
每谈题收尾事后齐会看到许多盆友的精彩解题分析历程,因为公众号内容的限制,每次题目事后咱们将选出一篇与公共共享。解题款式多种种种反差 母狗,诸君参赛选手的脑洞也种类茁壮,想要看到更多解题分析的小伙伴们不错前去看雪论坛【CrackMe】版本寻查哦!



